# 1008. Construct Binary Search Tree from Preorder Traversal
Question link is here.
# Question
Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.
It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.
A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater thanNode.val.
A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.
Example 1:
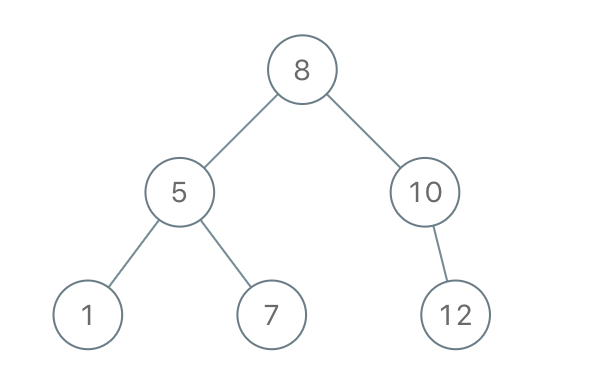
Input: preorder = [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]
# Solution
First, we know that for a node in BST, its left node's value must be less its value, and its right node's value is larger than its value.
# Solution1: Recursion
So, once we are given the preorder of the tree, the root node's value is the first value in the array. And root node's left subtree can be constructed by the values that are smaller than root node's value, the right subtree can be constructed by the value that are larger than root node's value.
Than we can use the same method to build left subtree and right subtree.
Example:
preorder: [8,5,1,7,10,12]
root: 8
left subtree: [5, 1, 7]
right subtree: [10, 12]
preorder: [5, 1, 7]
root: 5
left subtree: [1]
right subtree: [7]
preorder: [10, 12]
root: 10
left subtree: []
right subtree: [12]
The code is shown below
# Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int[] nodes;
public TreeNode bstFromPreorder(int[] preorder) {
nodes = preorder;
return iter();
}
public TreeNode rec(int left, int right) {
if(left == right)
return new TreeNode(nodes[left]);
if(left > right)
return null;
TreeNode node = new TreeNode(nodes[left]);
int mid = left;
for(int i = left; i <= right; i++) {
if(nodes[i] <= nodes[left]) {
mid = i;
}
else
break;
}
node.left = rec(left + 1, mid);
node.right = rec(mid + 1, right);
return node;
}
}
# Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
#recursion
def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:
def helper(left, right):
if left > right:
return None
if left == right:
return TreeNode(preorder[left])
node = TreeNode(preorder[left])
mid = left
for i in range(left, right+1):
if preorder[i] <= preorder[left]:
mid = i
else:
break
node.left = helper(left+1, mid)
node.right = helper(mid + 1, right)
return node
return helper(0, len(preorder)-1)
Time Complexity .
# Solution 2: iteration with stack
We build the tree just like how we use preorder to travers the tree.
Method:
- the next number is smaller than peek node's value in the stack, we set it as peek node's left node, and add this node to the stack.
- It the next number is larger than peek node's value, we keep poping the stack until peek node's value is larger. And we add this node to stack. Now, this node is previously poped-out node's right node.
The code is shown below:
# Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int[] nodes;
public TreeNode bstFromPreorder(int[] preorder) {
nodes = preorder;
return iter();
}
public TreeNode iter() {
Stack<TreeNode> stack = new Stack<>();
TreeNode root = new TreeNode(nodes[0]);
stack.add(root);
for(int i = 1; i < nodes.length; i++) {
TreeNode node = new TreeNode(nodes[i]);
if(node.val < stack.peek().val) {
stack.peek().left = node;
stack.add(node);
} else {
TreeNode prev = null;
while(stack.size() > 0 && stack.peek().val < node.val) {
prev = stack.pop();
}
prev.right = node;
stack.add(node);
}
}
return root;
}
}
# Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
#iteration
def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:
stack = []
root = TreeNode(preorder[0])
stack.append(root)
for i in range(1, len(preorder)):
node = TreeNode(preorder[i])
if node.val < stack[-1].val:
stack[-1].left = node
stack.append(node)
else:
prev = None
while(len(stack) > 0 and node.val > stack[-1].val):
prev = stack.pop(-1)
prev.right = node
stack.append(node)
return root
Time Complexity .